Anualidades anticipadas II
La diferencia entre las dos anualidades consiste en que la serie de la anualidad ordinaria empieza con 1 y termina con (1+i)^(n-1), en cambio, la serie de anualidad anticipada comienza con (1+i) y termina con (1+i)^n. Si a la serie anticipada se le agrega un 1 y se le resta al final, el resultado no se altera, siendo esta operación como sigue:
Se debe observar que la parte que está dentro del paréntesis es igual a la serie ordinaria, por lo tanto, se puede expresar que:
Si se reemplaza Sn┐i por su equivalente ((1+i)n-1)/i, se tendrá:
Si se factoriza ((1+i)n-1), se tendrá:
Si se factoriza ((1+i)n-1), se tendrá:
Que es equivalente a: (F/A,n,i%)(1+i)
Anualidades anticipadas I
Como ya se dijo, una anualidad anticipada es aquella en que los pagos se hacen al principio del período. El valor presente y el valor final se representarán respectivamente de la siguiente manera:
Los dos puntos o diéresis indican que es anticipado.
Existen relaciones entre las anualidades ordinarias y las anualidades anticipadas, las cuales pueden ser deducidas del análisis de las siguientes gráficas:
Para facilitar el planteamiento de la ecuación de valor se comienza con el pago que está en n, siguiendo con el que está en n-1 y así sucesivamente hasta llegar al pago situado en 1, entonces para el valor final con anualidad ordinaria la ecuación de valor quedará de la siguiente forma:
Sn┐i = 1+ (1+i) + (1+i)2 + … + (1+i)n
Para la anualidad anticipada en valor final, la gráfica del flujo de caja quedará de la siguiente manera:
Obsérvese que en el caso planteado se ha usado una doble numeración la que está por encima de la línea de tiempo indica el número de pago, mientras que la que se encuentra debajo de la línea de tiempo señala los períodos y así en el período 0 que es el comienzo del primer período se está haciendo el pago número 1, en el período 1 que es el final del primer período pero a su vez es el comienzo del segundo período y por eso se realiza el segundo pago y así sucesivamente hasta que se llegue al punto n-1 debajo de la línea de tiempo que representa el final del período n-1 pero también es el comienzo del período n y por tanto ahí debe estar el pago n y su ecuación de valor será:
Ejemplo 3 - Anualidades ordinarias – Valor presente y valor futuro
Una deuda e 50000 $ se va a cancelar mediante 12 pagos uniformes de R $. Con una tasa de 2 % efectivo para el período, encontrar el valor de la cuota R situando la fecha focal en:
a) El día de hoy
b) En 12 meses
Solución:
a) Si se pone la fecha focal el día de hoy, la gráfica que representa el flujo de fondos será la siguiente:
Para este primer caso se usará la siguiente expresión:
an┐i
Ya que todo el flujo de caja debe ser puesto al principio que es donde está la fecha focal y la ecuación de valor quedará de la siguiente manera:
50000 = Ra12┐2%
De donde:
El valor de la renta será igual a:
R = 4727.98 $
b) Si se pone la fecha focal en 12 meses la gráfica correspondiente al flujo de caja para el ejemplo planteado será:
En este caso se puede emplear la siguiente expresión: Sn┐i
Ya que todo el flujo de caja debe ser puesto en el punto 12 que es donde está la fecha focal, pero la deuda de los 50000 $ sigue en 0, lo cual implica que deberá ser trasladada a valor final junto con todos los pagos, entonces la ecuación quedará de la siguiente manera:
50000(1.02)12 = R S12┐2%
Resolviendo la ecuación anterior para R se obtiene:
R = 4727.98 $
Nótese que los valores obtenidos usando las dos fechas focales son iguales.
Ejemplo 1 Anualidades ordinarias – Valor presente
Un documento estipula pagos trimestrales de 80000 $ durante 6 años. Si este documento se cancela con un solo pago de:
a) A $ al principio o,
b) S $ al final, con una tasa del 32 % CT.
Solución:
El número de pagos se puede calcular mediante:
n = 4*6= 24
Y R = 80000 $
La tasa efectiva trimestral será:
i = (32 % / 4) = 8 % efectivo trimestral
a)
La representación del flujo de caja correspondiente será:
Luego el valor del pago representado por A será:
A = 80000*[1-(1+0.08)-24]/0.08 = 842301 $
b)
El flujo de caja para el caso puede ser representado por:
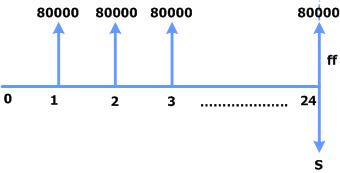
Luego el valor del pago equivalente a S se determinará de la siguiente manera:
S = 80000[1+0.08)24-1]/0.08 = 5341181 $
Anualidades ordinarias y anticipadas – El valor presente
Valor presente
El caso del valor presente se lo representa por an┐i en la notación actuarial y por (P/A,n,i%) en la notación tradicional y significará el valor presente de una anualidad de n pagos puestos en valor presente a la tasa i %.
La fórmula se obtiene al plantear la ecuación de valor con fecha focal al principio y trasladando todos los pagos a valor presente a la tasa i (de nuevo, no se pierde generalidad si se supone que todos los pagos son de 1$).
(P/A, n, i%) = an┐i = (1+i)-1+(1+i)-2+………+(1+i)-n
Para simplificar la ecuación anterior, se puede seguir un procedimiento similar al realizado para el valor final; sin embargo el camino mas corto consiste en actualizar el valor final.
Luego se tendrá:
an┐i = Sn┐i (1+i)-n
Si se reemplaza Sn┐i por su equivalente ((1+i)n-1)/i, se tendrá:
an┐i = [((1+i)n-1)/i](1+i)-n = [1-(1+i)-n)]/i
De donde se puede concluir que:
(P/A,n,i%) = an┐i = [1-(1+i)-n)]/i
Las anteriores fórmulas fueron deducidas para una renta de 1 $, pero si la renta hubiese sido de R $, el valor final VF o el valor presente VP hubiese sido R veces mayor. Por la tanto se puede escribir lo siguiente:
VF = R Sn┐i
Y también
VP = R an┐i
Plazo de una anualidad y Valor final II
Plazo de una anualidad (continuación)
Ahora se procederá a calcular el valor final de una anualidad. No se pierde generalidad si se supone que la renta es de 1 $, pues este valor puede ser factorizado en la ecuación para calcular el valor final, como se muestra a continuación en referencia a un ejemplo mostrado anteriormente:
2000000 = R[((1.1)-1+(1.1)-2+(1.1)-3+(1.1)-4]
Lo que está dentro de los corchetes es el valor presente de 1 $ en un período, seguido del valor presente de 1 $ en dos períodos y así sucesivamente hasta llegar al valor presente de 1 $ en 4 períodos.
En forma general se tendrá:
Para plantear la ecuación de valor con fecha focal en n se traslada cada uno de los pagos de 1 $ a valor final usando la fórmula del interés compuesto S= P(1+i)n a cada pago, pero en cada caso, P=1. El pago que está en 1 se traslada por n-1 períodos, el que está en 2 se traslada por n-2 períodos y así sucesivamente hasta llegar al pago que está en n, el cuál no se traslada por estar en la fecha focal, entonces se tendrá: (F/A, n, i%) = 1+ (1+i) + (1+i)2 + ……… + (1+i)n-1
Si se multiplica la ecuación anterior por (1+i) se obtendrá lo siguiente:
(F/A, n, i%) (1+i) = (1+i) + (1+i)2 + ……… + (1+i)n
Si se realiza la resta de las dos ecuaciones anteriores, se obtendrá:
(F/A, n, i%) (1+i) - (F/A, n, i%) = (1+i)n -1
Factorizando (F/A, n, i%) o Sn┐i en la notación actuarial, se obtiene:
(F/A, n, i%) (i) =(1+i)n -1
Por último despejando (F/A, n, i%), se tendrá:
(F/A, n, i%) = Sn┐i=((1+i)n-1)/i)
Plazo de una anualidad y Valor final
Plazo de una anualidad
El tiempo que transcurre entre el inicio del primer período y el final del último período se denomina el plazo de una anualidad y se representa por n.
Una anualidad tiene dos valores el valor final y el valor presente en el primer caso, todos los pagos son trasladados al final de la anualidad y en el segundo caso todos los pagos son trasladados al principio de la anualidad.
Valor final
Si se hace los cálculos para hallar el valor final de una anualidad ordinaria. El valor final puede ser representado de dos maneras:
La primera usando la notación tradicional:
(F/A,n,i%)
Donde F significa valor final, A significa que se trata de una anualidad, n indica el número de pagos de la anualidad y la i % significa la tasa de interés a la cual todos los pagos son trasladados a valor final.
La segunda forma de representación es con la notación actuarial:
Donde la S significa valor final, la n (cantidad que se escribe dentro del ángulo) indica el número de pagos y la i indica la tasa de interés a la cual serán llevados todos los pagos a valor final.
Debido a que la notación actuarial es más condensada en muchos casos es recomendable su utilización.
Anualidades ordinarias y anticipadas VI
El siguiente gráfico no representa una anualidad porque hay 4 pagos y hay 5 períodos.
Claramente puede observarse que cuando se inicia el gráfico con pago y se termina con pago, no hay una anualidad bien conformada y cuando el gráfico inicia con período y termina con período, tampoco hay una anualidad bien conformada. Las gráficas que representan anualidades bien conformadas tienen una característica en común, que su inicio y fin son diferentes, en un caso se inicia con período y se termina con pago y en el otro se inicia con pago y se termina con período.
En conclusión se puede decir que para una anualidad este bien conformada, en la grafica de representación el inicio y el fin deben ser diferentes.
Anualidades ordinarias y anticipadas V
Anualidad ordinaria o anualidad vencida
Para que la gráfica anterior represente una anualidad bien conformada es necesario agregarle un período que bien puede quedar al principio o al final. En el primer caso se tendría:
La anualidad así conformada recibe el nombre de anualidad ordinaria o anualidad vencida que viene a ser aquella en que los pagos se efectúan al final del período por ejemplo el pago de los sueldos de un empleado (primero viene el período de trabajo y después viene el pago). Anualidad anticipada
En el segundo caso se tendría:
Las anualidades así conformadas reciben el nombre de anualidades anticipadas porque los pagos se efectúan al principio del período por ejemplo el pago mensual del arriendo de una casa (primero paga y después tiene derecho a ocupar la casa durante el mes que se pagó).
Anualidades ordinarias y anticipadas IV
La segunda condición establece que los pagos deben hacerse a iguales intervalos de tiempo, esto es necesario para que los exponentes sean ascendentes o descendentes tal como se vio en las ecuaciones del ejemplo señalado. Esta condición se cumple aún si los pagos son trimestralmente, semestralmente o anualmente y sin embargo a la serie se le sigue llamando anualidad.
La tercera condición establece que todos los pagos deben ser llevados a valor presente o a valor final, según sea el caso, a la misma tasa de interés. Esto garantiza que todos los términos dentro del paréntesis tienen la misma base, por lo tanto, la serie que está adentro del paréntesis forma una progresión geométrica.
La cuarta condición establece que el número de pagos debe ser igual al número de períodos.
Por lo tanto la serie que se muestra en la siguiente gráfica no representa una anualidad porque tiene 4 pagos y solo hay 3 periodos.
Anualidades ordinarias y anticipadas III – Renta, período de renta, anualidad
Renta
Es el pago periódico de igual valor que corresponde a los R $ del ejemplo anterior. A la renta también se le conoce con el nombre de: cuota, depósito, retiro o pago, según sea el caso.
Período de renta
Es el tiempo que transcurre entre dos pagos periódicos consecutivos.
Anualidad
Una anualidad es una serie de pagos que cumple con las siguientes condiciones:
- Todos los pagos son de igual valor.
- Todos los pagos se hacen a iguales intervalos de tiempo.
- A todos los pagos se les aplica la misma tasa de interés.
- El número de pagos es igual al número de períodos.
Las condiciones anteriores obedecen a ciertas normas y tienen algunas implicaciones, por ejemplo, la primera condiciones es indispensable para poder factorizar tal como se hizo cuando se plantearon las ecuaciones de valor del ejemplo inicial mostrado en la introducción del tema de anualidades.
Anualidades ordinarias y anticipadas II
Si se hubiese planteado la ecuación de valor con fecha focal al final la ecuación de valor habría quedado de la siguiente manera:
2000000(1.14) = R(1+0.1)0+R(1+0.1)1+R(1+0.1)2+R(1+0.1)3
Factorizando se tendría:
2000000(1.14) = R((1+0.1)0+(1+0.1)1+(1+0.1)2+(1+0.1)3)
Luego: 2898200 = R(4.641)
R = 630941.61 $
Se observa a primera vista que la ecuación tiene una presentación muy distinta pero el resultado final es el mismo.
El problema anterior no presentó dificultad en su resolución, pero, si el número de pagos hubiese aumentado considerablemente, la solución no hubiese sido tan sencilla, como en el caso de pagar una deuda mediante pagos mensuales, durante 20 años. La solución de este problema dio origen a un modelo matemático llamado anualidad. A continuación se darán algunas definiciones básicas para el tema de anualidades.
Anualidades ordinarias y anticipadas I
Considere el siguiente ejemplo:
Ejemplo:
Una persona compra un terreno cuyo valor, al contado, es de 2 millones de $. Si le dan la facilidad para pagarlo en cuatro cuotas trimestrales de R $ cada una, que se efectuarán al final de cada trimestre y además se le cargaría un interés del 40 % CT, hallar el valor de la cuota trimestral de amortización.
Solución:
En primera instancia se puede construir un grafico en el que se represente los flujos de dinero establecidos en el ejemplo. Este gráfico se conoce también con el nombre de flujo de caja. Puesto que la tasa tiene efectividad trimestral y los pagos son trimestrales se puede usar el trimestre como período.
Si se plantea la ecuación del valor poniendo la fecha focal en el año cero, la ecuación quedaría de la siguiente forma: 2000000 = R(1+0.1)-1+R(1+0.1)-2+R(1+0.1)-3+R(1+0.1)-4
Factorizando R se tendría:
2000000 = R((1+0.1)-1+(1+0.1)-2+(1+0.1)-3+(1+0.1)-4)
Haciendo cálculos:
2000000 = R(3.169865)
Despejando el valor de la cuota se tendría:
R = 630941.61 $
Solución ejercicios propuestos tasas de interes libro Tarkin y Blank III
Ejercicio
Calcule la cantidad de interés por pagar después de 1 año sobre un préstamo de $5000 si el interés es 8 % anual. ¿Cuál es el periodo de interés?
Solución:
El interés se puede calcular mediante:
Interés = Monto adeudado al final – Monto original del préstamo
El monto adeudado al final será igual a:
Monto adeudado al final = Monto original del préstamo * (1+tasa de interés)
Reemplazando valores:
Monto adeudado al final = $5000 * (1.08) = $5400
Luego el interés será:
Interés = $5400 - $5000 = $400
Alternativamente se puede hacer el siguiente procedimiento.
La cantidad de interés a pagar por el préstamo de $5000 al 8 5 anual será igual a:
Interés = tasa de interés * monto del préstamo
Reemplazando valores se tendrá:
Interés = 0.08 * $5000 = $400
El período de interés será igual a 12 meses.
Solución ejercicios propuestos tasas de interes libro Tarkin y Blank II
Ejercicio
Cheryl reunió tasas de préstamo promocionadas de tres lugares. Estas son: 10 % anual compuesto semestralmente, 11 % anual compuesto trimestralmente y 11.5 % anual. Establezca el periodo de interés en meses para cada tasa.
Solución:
De acuerdo al enunciado del ejercicio, los períodos de interés en meses para cada tasa serán.
10 % anual compuesto semestralmente corresponderá a períodos de 6 meses.
11 % anual compuesto trimestralmente corresponderá a períodos de 3 meses
11.5 % anual, corresponderá a períodos de 12 meses.
Solución ejercicios propuestos tasas de interes libro Tarkin y Blank I
Ejercicio
Julio obtuvo un préstamo de $1000 de un banco y pagó 12 % anual compuesto semestralmente. El rembolsó el préstamo en seis pagos iguales de $ 203.36 cada uno. Determine la suma total en dólares pagada por Julio y establezca que porcentaje del préstamo original representa este interés:
Solución:
Si se reembolsó el préstamo es seis pagos iguales de $203.36, la suma total desembolsada por Julio será:
Monto total desembolsado = $203.36 * 6 = $1220.16
El interés pagado en términos monetarios, respecto al monto del préstamo obtenido será igual a:
Interés = Monto pagado – Monto préstamo original
Reemplazando valores se tiene:
Interés = $1220.16 - $1000 = $220.16
El porcentaje del interés pagado respecto al monto del préstamo original será entonces:
% préstamo original que representa el interés pagado = ($220.16/$1000)*100% =22.016 %
Ejemplo calculo de tasas de interes:
a) Calcular la suma de dinero que debe haber sido depositada hace 1 año para tener ahora $100 a una tasa de interés del 5% anual.
b) Calcular los intereses ganados durante el periodo de tiempo señalado
Solución:
a) La cantidad total acumulada es la suma del depósito original y el interés ganado. Si X es el depósito original,
Total acumulado = original + original (tasa de interés)
$100=X+ X(0.05)=X(1+0.05)= 1.05X
El depósito original es X, luego despejando su valor de la igualdad planteada con anteriodad, se obtiene:
X = (100/1.05) $
X = 95.238 $
b) Los intereses ganados estarán determinados por la cantidad final que se tiene (100 $) menos la cantidad inicial depositada.
Por lo que el interés ganado será igual a:
Interés ganado = 100 $ - 95.238 $ = 4.762 $
Ejemplo 2 equivalencias tasas de interés referenciales
Ejemplo
Un industrial tiene actualmente contratado un préstamo con una corporación financiera a la tasa referencial T + 3 puntos. ¿Cuál debe ser el spread en puntos básicos de forma tal que financieramente sea indiferente el préstamo en la corporación financiera o en el mercado de Londres?
Suponga los siguientes datos:
Tasa referencial T = 15.3 % TA
idevaluación= 22 % EA
Tasa libor =5.2 % EA
Solución:
El préstamo que se realice en Londres se efectuará en Libras Esterlinas y obviamente una devaluación del peso frente a la libra esterlina afectará al costo del crédito, por tal razón, la siguiente ecuación incluye la tasa de devaluación.
idevaluación + (tasa libor + X) = Tasa referencial + 3
Si se trabaja el miembro de la derecha de la anterior igualdad se tendrá:
Tasa refencial + 3 = 15.3 % TA + 3 % TA = 18.3 % TA (puesto que son tasas nominales, se pueden sumar directamente).
Por equivalencia de tasas se puede convertir la tasa nominal trimestre anticipado en una tasa efectiva anual, obteniéndose el siguiente resultado:
18.3 % NTA = 20.601 % EA
Si se trabaja el miembro izquierdo de la igualdad inicial planteada se tendrá:
idevaluación + (tasa libor + X) = 22 % + (5.2+X) %
(5.2+X) % puede ser escrita como (5.2+X)/100 = 0.052 + 0.0X
La suma del 22 % y del (5.2+X) % debe realizarse usando la combinación de tasas de la siguiente manera:
22 % + (5.2+X) % + 22 % (5.2+X) % = 0.22 + 0.052 + 0.0 X + (0.22)(0.052) + 0.0022 X
Reduciendo términos semejantes resulta:
0.28344 + 0.0122X
Igualando el miembro de la izquierda y la derecha de la igualdad inicial planteada, se tendrá:
0.28344+0.0122X = 0.20601
Despejando X, se tendrá:
X=-6.35 %
Lo que significa que cobrar una tasa referencial + 3 puntos es lo mismo que cobrar devaluación más libor menos 6.35 puntos.
Ejemplo equivalencias tasas de interés referenciales
Supóngase que una persona tiene un préstamo hipotecario al IPC + 4 puntos. ¿Cuál debe ser el spread si se cambia a otro plan cuya tasa es una tasa referencial + X? Suponga que el IPC es igual a 8 % y que la tasa referencial igual a 18.67 % TA (Trimestre anticipado).
Solución:
Se plantea la siguiente ecuación:
IPC + 4 = Tasa referencial + X
Pero se debe tener en cuenta que el IPC tiene efectividad anual, mientras que la Tasa referencial está dada como nominal trimestre anticipada.
La igualdad debe realizarse en las mismas unidades y el spread en cada caso viene a quedar en las mismas unidades de la tasa principal, en este caso 4 viene a ser efectivo anual y X viene a ser nominal trimestral anticipada.
Se debe recordar que para sumar dos tasas efectivas se aplica la fórmula de tasa combinadas, por tanto el primer miembro de la igualdad dada con anterioridad será:
IPC + 4 = 0.08 + 0.04 + 0.08*0.04 = 0.1232 =12.32 % efectivo anual
Como la incógnita que está en el otro miembro de la ecuación está dada en nominal trimestre anticipado entonces esta tasa debe ser convertida en nominal trimestre anticipado:
(1+0.1232) = (1+i)4 de donde:
i = 2.9471 % período trimestre vencido
Luego:
ia = i/(1+i) = 0.029741/(1+0.029741) = 2.86275 % TA
Y entonces:
ja = 2.68275*4 =11.451 % TA
Y el anterior valor corresponde al primer miembro de la igualdad IPC + 4 = Tasa referencial + X.
La suma de dos tasas nominales se obtiene efectuando una suma simple de manera que el segundo miembro de la ecuación anterior será:
Tasa referencial + X = 0.187 + X nominal trimestre anticipado
Finalmente la ecuación quedará de la siguiente manera:
0.11451 = 0.1867 + X
De donde:
X = -0.07219 = -7.219 % TA
De donde se puede concluir que si se cambia de plan tendrá que ser a la Tasa referencial menos 7.219 %.
Equivalencia de tasas de interés referenciales
Hay muchos créditos atados a una tasa principal por ejemplo a la inflación más unos puntos adicionales, estos puntos adicionales se denominan el Spread, suponiendo que la inflación fuera del 10 % efectivo anual y el que spread sea de 5 puntos, entonces la tasa a la cual se cancelaría el crédito se puede calcular aplicando la fórmula de la tasa combinadas:
i = 0.1+0.05+0.1*0.05 = 0.155 = 15.5 % efectivo anual
Cuando la tasa principal viene dada en forma efectiva anual para agregarle el spread se usa la fórmula de combinación de tasas pero si el spread se le adiciona a una tasa de interés nominal entonces el spread simplemente se suma a la tasa principal por ejemplo:
Si un préstamo para vivienda se otorga a la tasa principal X más 8 puntos y suponiendo que la tasa de interés X = 17 % TA (significa 17 % nominal trimestre anticipado), entonces la tasa del crédito será:
0.17 + 0.08 = 0.25 = 25 % TA
Por equivalencia de tasas se concluye que es equivalente al 29.5 % efectivo anual.
Si se reemplaza Sn┐i por su equivalente ((1+i)n-1)/i, se tendrá:
Que es equivalente a: (F/A,n,i%)(1+i)
