Definición de tasa de interés
El origen del fenómeno de la tasa de interés se encuentra en la disyuntiva existente entre el poder adquisitivo presente y futuro. La tasa de interés es el precio que se debe pagar por el crédito y, al igual que otros precios, cumple una función asignadota (o de racionamiento). La tasa de interés le ayuda a la sociedad a decidir cómo asignar la producción de bienes y servicios a través del tiempo.
Al igual que otros precios, la tasa de interés también proporciona información. A escala nacional, la tasa de interés refleja la tasa de preferencia en el tiempo de la comunidad en cuanto al consumo de bienes y servicios. Manteniendo constantes otros factores, una tasa de interés relativamente alta indica que la comunidad está impaciente y desea consumir más en el presente. Dado que los restantes factores se mantienen constantes, una tasa de interés relativamente baja refleja una sociedad paciente, orientada hacia el futuro, que se muestra dispuesta a renunciar al consumo presente para tener un mayor consumo futuro.
La tasa de interés les permite a las personas comparar valores presentes con valores futuros porque, por su misma naturaleza ella refleja la disyuntiva existente entre poder adquisitivo presente y futuro. Las distintas familias tienen diferentes preferencias en el tiempo en cuanto a sus niveles de consumo y, dados sus gustos en cuanto a intercambiar consumo presente por consumo futuro, preferirán ahorrar y prestar un porcentaje de sus ingresos. A esa misma tasa de interés, algunas familias preferirán convertirse en prestatarias netas. Esas familias preferirán un consumo superior a su ingreso en el presente, sabiendo que deberán sacrificar consumo futuro, porque tendrán que devolver el interés y el capital (cantidad que se toma en préstamo).
En igual forma, las distintas empresas tienen expectativas diferentes en cuanto a ganancias; a una determinada tasa de interés, una empresa A tomará dinero en préstamo si espera obtener una tasa de ganancias superior a la tasa de interés; ésta otorgará préstamos si espera obtener una tasa de ganancia inferior a la tasa de interés.
Teniendo en cuenta que las familias tienen distintas tasas de preferencias en el tiempo en cuanto a consumo y, que las empresas tienen diferentes expectativas de ganancias, dada una determinada tasa de interés, ciertas unidades económicas se convertirán en prestamistas netos y otras, en prestatarios netos. Esto significa que unas familias serán prestamistas netas y otras prestatarias netas y que algunas empresas serán prestamistas netas y otras prestatarias netas.
Ejemplo 4 de cálculo equivalencia entre tasas de interés – Gráfica equivalencia tasas de interés Ejemplo:
Dado 20 % período 200 días anticipado, calcular una tasa de interés nominal vencida con período 150 días.
Solución:
La tasa con período 200 días anticipada se representará por ia.
Saliendo del punto 6 de la gráfica de equivalencia de tasas de interés se llegará al punto 4.
En el punto 6, ia = 20 % en el punto 2 i = ia / (1-ia) = 0.2 / (1-0.2) = 0.25
Para el paso de 2 al punto 3 se debe tener en cuenta que si un período tiene 200 días entonces habrá en 1 año 365 / 200 períodos, en igual forma, si un período tiene 150 días en un año habrá 365 / 150 períodos, por lo tanto se puede plantear la siguiente ecuación: (1+0.25)365/200 = (1+i2)365/150
Despejando la tasa de interés del lado derecho de la ecuación anterior, se tendrá:
i = 18.2177 % período 150 días que corresponde al punto 3.
Para llegar al punto 4 se aplica la fórmula:
j = i * m
Entonces reemplazando valores se obtendrá:
j = 18.2177 * (365/150) = 44.33 % N150dv
Ejemplo 3 de cálculo equivalencia entre tasas de interés – Gráfica equivalencia tasas de interés
Ejemplo:
Dado el 28 % nominal con período de 258 días hallar una tasa efectiva anual.
Solución:
La tasa nominal con intereses vencidos pagaderos por períodos de 258 días se la puede representar por: N258dv.
En la gráfica de equivalencia de tasas, se inicia en 1 se va al punto 3.
En 1 j=N258dv
Para llegar a 2 se sabe que i = j / m. Como el período tiene 258 días, entonces en un año habrá 365 / 258 =1.4147 períodos y al reemplazar en la fórmula señalada se tendrá:
i = 0.28 / 1.4147 =0.1979 =19.79 % período 258 días
Para el paso del punto 2 al punto 3, se tendrá:
(1+0.1979)365/258 = (1+i2)1
Despejando la tasa de interés se tendrá:
i = 29.10797 % efectivo anual
Ejemplo 1 de cálculo equivalencia entre tasas de interés – Gráfica equivalencia tasas de interés
Ejemplo:
Dado el 30 % nominal trimestre anticipado, calcular una tasa efectiva mensual anticipada que sea equivalente.
Solución:
En la gráfica de equivalencia de tasas, se sitúa el punto 5 como punto de partida que corresponde a una tasa nominal anticipada y el destino final será el punto 7, que corresponde a una tasa efectiva anticipada.
En el punto 5 ja=30 % NTA En el punto 6:
ia = ja / m = 30 / 4 = 7.50% trimestre anticipado
Para llegar al punto 2 se aplica la fórmula:
i = ia / (1- ia)
Reemplazando los valores de la tasa de interés encontrada.
i = 0.075 / (1- 0.075) = 8.1081 % trimestral
El paso de 2 a 3 implica el planteo de la ecuación:
(1+0.081081)4 = (1+i2)12
Obsérvese que el primer paréntesis quedó elevado a la potencia 4 porque la tasa tiene efectividad trimestral y el segundo paréntesis quedó elevado a la potencia 12 porque los nuevos períodos deben ser meses, así:
i = 2.6328 % EM
El paso de 3 a 7 implica el planteo de la ecuación.
ia = i / (1- i) = 0.026328 / (1+0.026328) = 2.565 % EMA =2.565 % periódica mes anticipado
Ejemplo de cálculo equivalencia entre tasas de interés – Gráfica equivalencia tasas de interés
Ejemplo:
Dada la tasa de interés del 36 % nominal mensual, encontrar:
a. Una tasa efectiva anual
b. Una tasa nominal semestral
c. Una tasa efectiva bimestral
d. Una tasa nominal semestral anticipada
Solución:
Empleando la gráfica de equivalencia de tasas de interés se tendrá:
a)
En el punto 1, j = 36 % NM (Nominal Mensual)
En el punto 2, i = j / m = 36 / 12 = 3 % EM (Efectivo Mensual)
Para el paso del punto 2 al punto 3, se plantea la ecuación:
(1+0.03)12 = (1+i2)1
Obsérvese que el primer paréntesis se eleva a la potencia 12 porque la tasa del 3 % tiene periodicidad mensual y en un año hay 12 períodos; el segundo paréntesis se eleva a la potencia 1 porque la tasa debe tener una periodicidad anual, es decir una efectividad anual; al despejar i de la ecuación anterior se obtiene que la tasa de interés buscada será:
i = 42.5761 % EA (Efectivo Anual)
b)
El punto de partida es el punto 1 y el punto de llegada debe ser el punto 4.
En el punto 1, j = 36 % NM (Nominal Mensual)
En el punto 2 i =j / m = 36 / 12 = 3 % mensual
Para el paso del punto 2 al punto 3 se plantea la siguiente ecuación:
(1+0.03)12 = (1+i2)2
Obsérvese que el segundo paréntesis se elevó a la potencia 2 porque la tasa debe tener una efectividad semestral y en un año hay 2 semestres. Al despejar i de la anterior ecuación se tendrá:
i = 19.4052 % ES (Efectivo Semestral)
Para el paso del punto 3 al punto 4, simplemente se multiplica el resultado anterior por 2, y así se tiene:
j = 19.4052 % * 2 = 38.81 % NM (Nominal Semestral)
c)
El punto de partida es el punto 1 y el punto de llegada es el punto 3.
En los puntos 1 y 2 se tienen los mismos resultados de los incisos a) o b) del ejemplo, por consiguiente en el punto 2, la tasa de interés efectiva es: i = 3 % EM (Efectivo Mensual)
El paso del punto 2 al 3, implica el planteo de la siguiente relación:
(1+0.03)12 = (1+i2)6
Obsérvese que el exponente del segundo paréntesis debe ser 6 porque se quiere trabajar con períodos bimestrales y en un año hay 6 bimestres. Al despejar se obtiene:
i = 6.09 % EB (Efectivo Bimestral) que también se puede escribir como 6.09 % período semestral.
d)
El punto inicial es el 1 y el punto de llegada debe ser el punto 8.
En los puntos 1 y 2 los resultados son los mismos que los mostrados en los incisos a), b) o c) del ejemplo.
El paso del punto 2 al punto 3 implica el planteamiento de la siguiente ecuación.
(1+0.03)12 = (1+i2)2
Despejando la tasa de interés buscada se tiene.
i = 19.4052 % ES (Efectivo Semestral)
El paso del punto 3 al punto 7 implica plantear la ecuación:
ia = i / (1+i)
Reemplazando valores en la anterior relación se tiene:
ia = 0.194052 / (1+0.194052) = 16.2516 % periódica semestral anticipada
El paso del punto 7 al punto 8, implica multiplicar el anterior resultado por 2 y se tendrá:
ja = 16.2516 *2 = 32.5 % NSA (Nominal Semestral Anticipada)
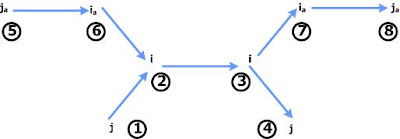
Gráfica de equivalencia de tasas de interés
Los puntos que se colocan en la gráfica (del 1 al 8), solo sirven para identificación y no es más que una ampliación de una gráfica mostrada con anterioridad.
La gráfica puede ser representada de la siguiente manera:
Donde: i = tasa ordinaria o vencida
ia = tasa efectiva anticipada (tasa periódica anticipada)
j = tasa nominal vencida
ja = tasa nominal anticipada
Nota:
Para el uso de la gráfica de equivalencia de tasas de interés, siempre se debe comenzar de un punto de la izquierda y seguir la trayectoria hasta llegar a otro punto situado en la parte de la derecha.
Relación entre una tasa de interés anticipada y una tasa de interés vencida
La tasa de interés viene a ser la relación entre el interés ganado sobre el capital invertido, lo que significa que:
i =I / P
Según la fórmula del valor líquido o valor de transacción visto con anterioridad, se tiene que:
VL = S (1-dt)
Entonces, al final de un período VL = S(1-d) y teniendo en cuenta que P viene a ser el valor líquido se tendrá:
i = I / P = (Sd) / S (1-d) = d / (1-d)
Como la tasa anticipada es la misma tasa de descuento, se tiene que conociendo una tasa anticipada se puede hallar la tasa vencida aplicando la fórmula:
i = d / (1-d)
La tasa d es una tasa de descuento que equivale a una tasa anticipada, por esta razón se la puede representar por ia, de tal forma que la ecuación anterior se puede escribir como:
i = ia / (1- ia)
Si se despeja ia de la anterior fórmula se llega a:
ia = i / (1+i)
Naturalmente también existen las tasas nominales anticipadas que se representarán por ja y por similitud con las tasas de interés vencidas se tendrá:
ja = ia*m
Y también
ia = ja / m
